进制也就是进位计数制,是人为定义的带进位的计数方法。对于任何一种进制如:X进制,就表示每一位上的数运算时都是逢X进一位。十进制是逢十进一,十六进制是逢十六进一,二进制就是逢二进一,以此类推,x进制就是逢x进位。
对于任何一个数,我们可以用不同的进位制来表示。比如:十进数57(10),可以用二进制表示为111001(2),也可以用五进制表示为212(5),也可以用八进制表示为71(8)、用十六进制表示为39(16),它们所代表的数值都是一样的。
十进制
十进制编码几乎就是数值本身。数值本身是一个数学上的抽象概念。经过长期的演化、融合、选择、淘汰,系统简便、功能全面的十进制计数法成为人类文化中主流的计数方法。
十进制数的书写可以不加标注,或加后缀D,其中D是英文十进制Decimal的首字母D。
十进制的基数为10,数码由0-9组成,计数规律逢十进一。
二进制
二进制由两个数码0,1组成,运算规律是逢二进一。
二进制数的书写通常在数的右下方注上基数2,或在后缀加B表示,其中B是英文二进制Binary的首字母。如:二进制数10110011可以写成(10110011)2,或写成10110011B。
计算机领域我们之所以采用二进制进行计数,是因为二进制具有以下优点:
- 二进制数中只有两个数码0和1,可用具有两个不同稳定状态的元器件来表示一位数码。例如,电路中某一通路的电流的有无,某一节点电压的高低,晶体管的导通和截止等。
- 二进制数运算简单,大大简化了计算中运算部件的结构。二进制数的加法和乘法基本运算法则各有四条,如下:
0+0=0,0+1=1,1+0=1,1+1=10
0×0=0,0×1=0,1×0=0,1×1=1 - 二进制天然兼容逻辑运算。二进制计数在日常使用上有个不便之处,就是位数往往很长,读写不便,如:把十进制的100000D写成二进制就是11000011010100000B,所以
计算机领域我们实际采用的是十六进制。二进制数转换为十六进制数时,长度缩减为原先的约四分之一,把十进制的100000写成八进制就是303240。十六进制的一个数位可代表二进制的四个数位。这样,十进制的100000写成十六进制就是186A0。
八进制
由于二进制数据的基数R较小,所以二进制数据的书写和阅读不方便,为此,在小型机中引入了八进制。八进制的基数R=8=2^3,有数码0、1、2、3、4、5、6、7组成,并且每个数码正好对应三位二进制数,所以八进制能很好地反映二进制。八进制用下标8或数据后面加O表示,如:二进制数据 (11 101 010 . 010 110 100)2 对应八进制数据 (352.264)8或352.264O。
十六进制
十六进制数由十六个数码:数字0~9加上字母A-F组成(A-F分别表示十进制数10~15),十六进制数运算规律是逢十六进一,即基数R=16=2^4。
通常在表示时用尾部标志H或下标16以示区别,在c语言中用添加前缀0x以表示十六进制数。如:十六进制数4AC8可写成(4AC8)16,或写成4AC8H。
进制转换
二进制转换
二进制转换八进制
不足三位,用'0'补齐,正数部分往左补齐,小数部分往右补齐
二进制转换十进制
幂取值以小数点为界往左为正0 ~ n,往右为负-1 ~ -n(如下图1/2、0/4、1/8….)
二进制转换十六进制
不足四位,用'0'补齐,正数部分往左补齐,小数部分往右补齐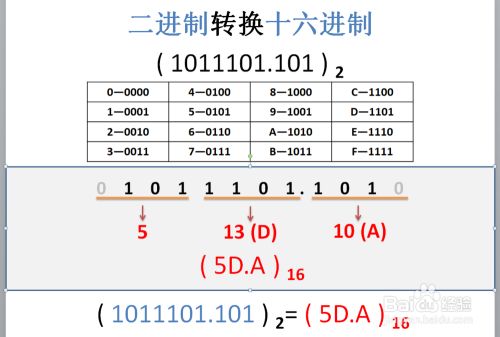
八进制转换
八进制转换二进制

八进制转换十进制

八进制转换十六进制

不足四位,用'0'补齐,正数部分往左补齐,小数部分往右补齐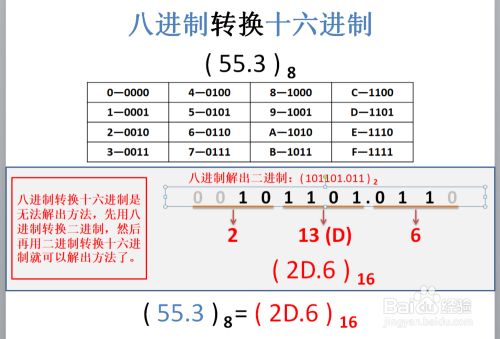
十进制转换
正数除以X进制,商至'0'为止;小数乘以X进制为正数为止
十进制转换二进制
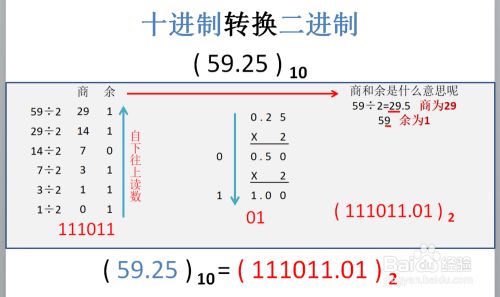
十进制转换八进制

十进制转换十六进制
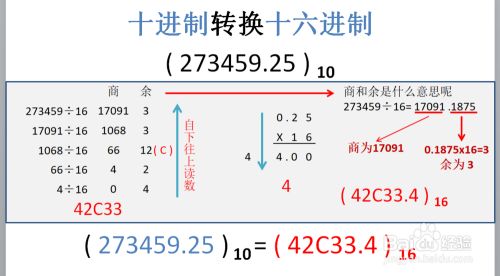
十六进制转换
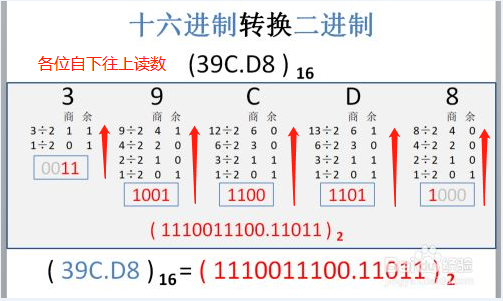
十六进制转换二进制
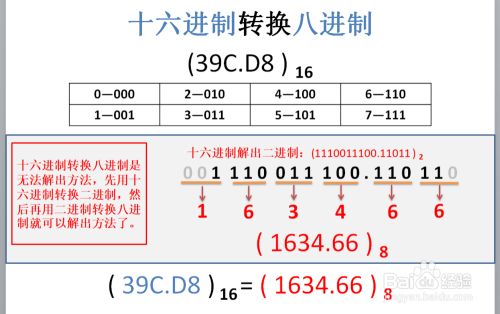
十六进制转换八进制
十六进制转换十进制

小技巧
十进制转八进制或者十六进制有两种方法
- 间接法
把十进制转成二进制,然后再由二进制转成八进制或者十六进制。这里不再做图片用法解释。- 直接法(本文使用方法)
把十进制转八进制或者十六进制按照除8或者16取余,直到商为0为止。
八进制与十六进制之间的转换有两种方法
- 以先转成二进制然后再相互转换(本文使用方法)。
- 先转成十进制然后再相互转换。